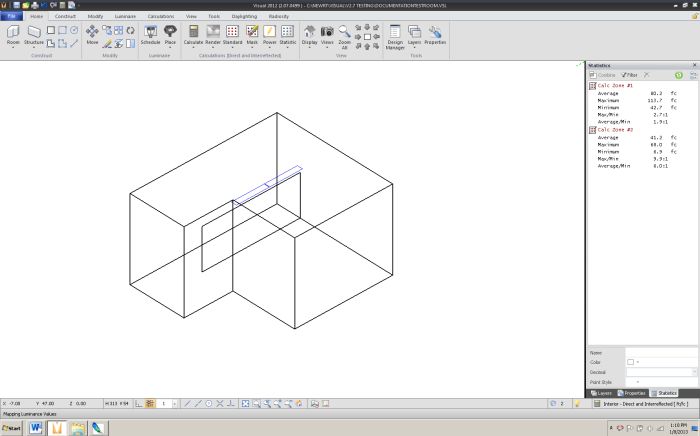
The first stage of user-specified surface discretization is purely geometric and involves two criteria: shape and proximity.
All surfaces handled by the Visual calculation engine are assumed to have four vertices, that is, they are planar quadrilaterals. User specified surfaces with more than four vertices are analyzed with three discretization algorithms; the best discretization is a balance between subsurface shape and number.

An L-shape room with a partition and two suspended linear direct luminaires
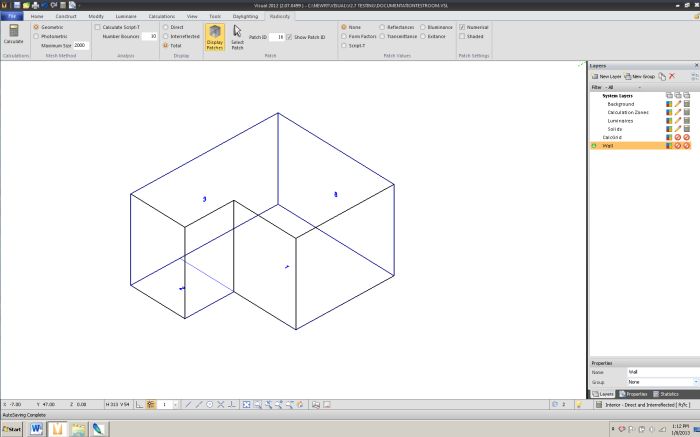
Shape discretization divides the floor and ceiling so that they are comprised of quadrilaterals.
The proximity criteria for discretization accounts for the presence of neighboring or intersecting surfaces are like to produce large exitance differences across the intersected surface.
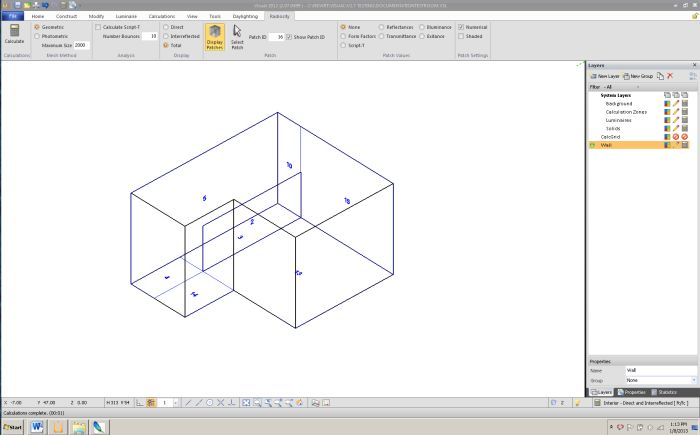
Proximity discretization further discretizes the floor and a wall since they are intersected by the partition.
After geometric and proximity, a third criterion is applied to further discretize subsurfaces: a discretization is made along any large illuminance gradients on a subsurface. An array of low-precision illuminances is calculated across a surface which consist of direct illuminance and illuminance produced by light reflected (only) once from other surfaces. Occlusion is accounted for. Neighboring illuminances are compared and if the ratio is greater than 3:1, the subsurface is further discretized there.
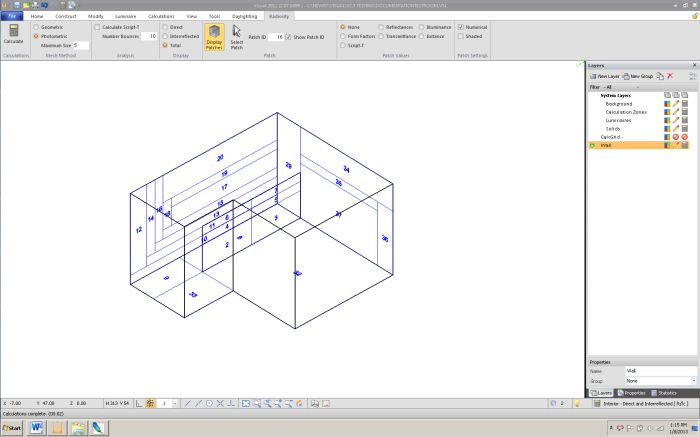
Photometric discretization finds large gradients in illuminance and further discretized subsurfaces. In this case, the walls contain gradients caused by both shadowing from the partition and the distribution of the luminaires.
These surfaces are a special case. Any user-specified surface with an image-preserving transmittance is not discretized for any reason.
Any user-specified surface with a diffuse transmittance is, like other surfaces, considered as two surfaces, back-to-back. In this case, the original coupling between the two is maintained throughout the entire computational process. If one surface of the pair is subjected to geometry or photometric discretization, that discretization is performed on its back-to-back partner. Thus, both surfaces are subject to discretization due to factors that affect either side. The result is a set of back-to-back subsurface pairs.